A vibration example with two modes
In the following example, we explore the a mechanical vibration example, especially with regard to its modes of vibration. Both undamped and (under)damped cases are considered and we discover the effects of damping.
Consider the system of figure 7.3 in which a velocity source VS is applied to spring K1, which connects to mass m1, which in turn is connected via spring K2 and damper B to mass m2 which.1
The state-space model A-matrix is given as $$\begin{aligned} A &= \begin{bmatrix} -B/m_1 & -1/m_1 & B/m_1 & 0 \\ K_1 & 0 & -K_1 & 0 \\ B/m_2 & 1/m_2 & -B/m_2 & -1/m_2 \\ 0 & 0 & K_2 & 0 \end{bmatrix} \end{aligned}$$ with parameters as follows:
m1 = 0.1 kg
m2 = 1.1 kg
K1 = 8 N/m
K2 = 9 N/m
Two different values for B will be considered: 0 and 20 N⋅s/m. We will explore the modes of vibration in each case and plot a corresponding free response.
This common situation appears in a slightly modified form in Rowell1997.↩︎
Setting up the problem
We analyze the problem with Python. First, we load packages for symbolic, numeric, and graphical analysis, as follow:
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
from pprint import pprintThe A matrix is first defined symbolically.
sp.var("m_1, m_2, K_1, K_2, B", real=True)
A = sp.Matrix([
[-B/m_1, -1/m_1, B/m_1, 0],
[K_1, 0, -K_1, 0],
[B/m_2, 1/m_2, -B/m_2, -1/m_2],
[0, 0, K_2, 0]
])Now define dictionaries for the parameter values.
p = {
m_1: 0.1, # kg
m_2: 1.1, # kg
K_1: 8, # N/m
K_2: 9 # N/m
}
pB1 = {B: 0} # N/(rad/s), without damping
pB2 = {B: 20} # N/(rad/s), with dampingWithout damping
Without damping, we expect the system to be marginally stable and
have two pairs of second-order undamped subsystems with their own unique
natural frequencies. The numerical A matrix can be computed by
substituting in the parameters in p
and pB1, as follows:
A_1 = np.array(A.subs(p).subs(pB1), dtype=float)
print(A_1)[[ 0. -10. 0. 0. ]
[ 8. 0. -8. 0. ]
[ 0. 0.90909091 0. -0.90909091]
[ 0. 0. 9. 0. ]]To explore the modes of vibration, we consider the eigendecomposition of A.
l_,M_ = np.linalg.eig(A_1)
thr = 1e-14 # threshold for calling something 0
l_.real[abs(l_.real) < thr] = 0.0 # zeroing small real partsLet’s take a closer look at the eigenvalues.
print(l_)[0.+9.38179379j 0.-9.38179379j 0.+2.726993j 0.-2.726993j ]So we have two pairs of purely imaginary eigenvalues. We would say, then, that there are two “modes of vibration,” and similarly two second-order systems comprising this fourth-order system. When we consider what the natural frequency and damping ratio is for each pair, we’re considering the natural frequencies associated with each “mode of vibration.”
For a second-order system (see section 6.3), the roots of the characteristic equation, which are equal to the eigenvalues corresponding to that second-order pair, are given in terms of natural frequency ωn and damping ratio ζ:
$$ -\omega_n\zeta \pm \omega_n \sqrt{\zeta^2-1}. $$
So the imaginary part is nonzero only when ζ ∈ [0, 1), that is, when the system is underdamped or undamped. In this case,
$$ -\omega_n\zeta \pm j \omega_n \sqrt{1-\zeta^2}. $$
This, taken with the fact that the eigenvalues in l_ have zero real parts, implies either
ωn or
ζ is zero. But if ωn is zero, the
eigenvalues would all be zero, which they are not. Therefore, ζ = 0 for both pairs of
eigenvalues.
This leaves us with eigenvalues: ± jωn1 and ± jωn2.
So we can easily identify the natural frequencies ωn1 and ωn2 associated with each mode as follows.
wn_1 = np.imag(l_[0]);
wn_2 = np.imag(l_[2]);
print(f"Natural frequencies (rad/s): {wn_1} and {wn_2}")Natural frequencies (rad/s): 9.38179378603641 and 2.726992997943728Free response
Let’s compute the free response to some initial conditions. The free state response is given by
x(t) = Φ(t)x(0).
So we can find this from the state transition matrix Φ, which is known from section 7.4 to be .
First, we construct Φ′ symbolically.
sp.var("t", real=True)
L = sp.diag(*list(sp.Matrix(l_)*t)) # Eigenvalue matrix Λ (symbolic)
M = sp.Matrix(M_) # Modal matrix (symbolic)
Phi_p = sp.exp(L)
pprint(Phi_p)Matrix([
[1.0*exp(9.38179378603641*I*t), 0, 0, 0],
[ 0, 1.0*exp(-9.38179378603641*I*t), 0, 0],
[ 0, 0, 1.0*exp(2.72699299794373*I*t), 0],
[ 0, 0, 0, 1.0*exp(-2.72699299794373*I*t)]])Now we can apply our transformation.
Phi = M*Phi_p*M.inv()So our symbolic solution is to multiply the initial conditions by this matrix.
x_0 = sp.Matrix([[1], [0], [0], [0]]) # Initial condition
x = Phi*x_0 # Free response (symbolic, messy)Plotting a free response
Let’s make the symbolic solution into something we can evaluate numerically and plot, a Numpy function.
x_fun = sp.lambdify(t,x)Now let’s set up our time array and state solution for the plot.
t_ = np.linspace(0,5,300)
x_ = np.squeeze(
np.real(x_fun(t_))
)Plot the state responses through time. The output is shown below.
fig, ax = plt.subplots()
ax.plot(t_, x_.T)
ax.set_xlabel('time (s)')
ax.set_ylabel('state free response')
ax.legend(['$x_1$', '$x_2$', '$x_3$', '$x_4$'])<matplotlib.legend.Legend at 0x127e64e30>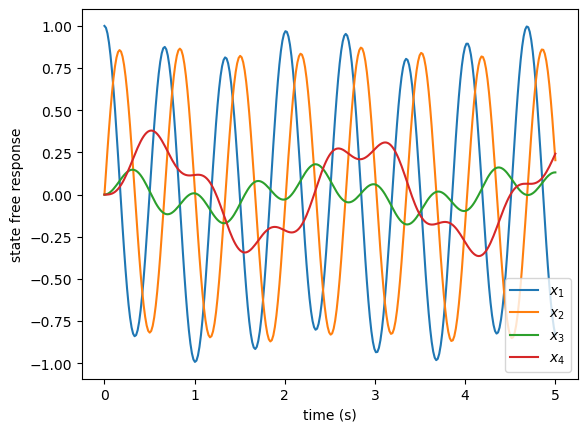
With a little damping
Now consider the case when the damping coefficent B is nonzero. Let’s recompute A and the eigendecomposition.
A_2 = np.array(A.subs(p).subs(pB2), dtype=float)
print(A_2)[[-200. -10. 200. 0. ]
[ 8. 0. -8. 0. ]
[ 18.18181818 0.90909091 -18.18181818 -0.90909091]
[ 0. 0. 9. 0. ]]To explore the modes of vibration, we consider the eigendecomposition of A.
l_,M_ = np.linalg.eig(A_2)Let’s take a closer look at the eigenvalues.
print(l_)[-2.17777946e+02+0.j -1.53514941e-03+2.73840736j
-1.53514941e-03-2.73840736j -4.00801807e-01+0.j ]We can see that one of the second-order systems is now “overdamped” or, equivalently, has split into two first-order systems. The other is now underdamped (but barely damped). Let’s compute the natural frequency of the remaining vibratory mode.
wn_1 = np.imag(l_[1]);
print(f"Natural frequency (rad/s): {wn_1}")Natural frequency (rad/s): 2.7384073593287575So the effect of damping was to eliminate the ≈ 10 rad/s mode and leave us with a slightly modified version of the ≈ 2.7 rad/s mode.
Free response
Let’s compute the free response to some initial conditions. The free state response is given by
x(t) = Φ(t)x(0).
So we can find this from the state transition matrix Φ, which is known from section 7.4 to be .
First, we construct Φ′ symbolically.
L = sp.diag(*list(sp.Matrix(l_)*t)) # Eigenvalue matrix Λ (symbolic)
M = sp.Matrix(M_) # Modal matrix (symbolic)
Phi_p = sp.exp(L)
pprint(Phi_p)Matrix([
[1.0*exp(-217.777946076145*t), 0, 0, 0],
[ 0, 1.0*exp(t*(-0.00153514941381959 + 2.73840735932876*I)), 0, 0],
[ 0, 0, 1.0*exp(t*(-0.00153514941381959 - 2.73840735932876*I)), 0],
[ 0, 0, 0, 1.0*exp(-0.400801806845378*t)]])Now we can apply our transformation.
Phi = M*Phi_p*M.inv()So our symbolic solution is to multiply the initial conditions by this matrix.
x_0 = sp.Matrix([[1], [0], [0], [0]]) # Initial condition
x = Phi*x_0 # Free response (symbolic, messy)Plotting a free response
Let’s make the symbolic solution into something we can evaluate numerically and plot, a Numpy function.
x_fun = sp.lambdify(t,x)Now let’s set up our time array and state solution for the plot.
t_ = np.linspace(0,5,300)
x_ = np.squeeze(
np.real(x_fun(t_))
)Plot the state responses through time. The output is shown below.
fig, ax = plt.subplots()
ax.plot(t_, x_.T)
ax.set_xlabel('time (s)')
ax.set_ylabel('state free response')
ax.legend(['$x_1$', '$x_2$', '$x_3$', '$x_4$'])<matplotlib.legend.Legend at 0x137a6acf0>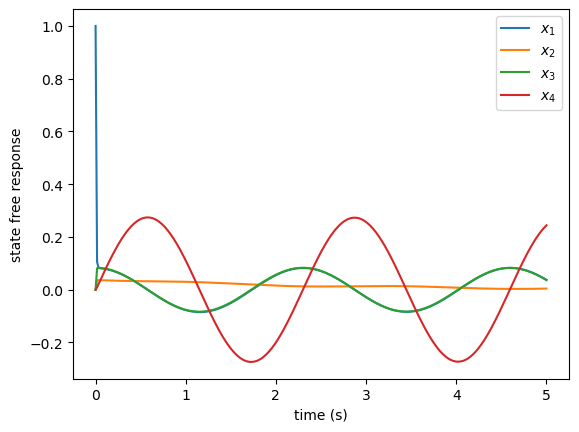
Online Resources for Section 7.5
No online resources.