Ideal transducers

Two-port system elements can model transducers—elements that transfer energy between two energy domains or change its form within an energy domain. The quintessential example, which we will consider in detail, is the motor, which converts electrical energy to mechanical energy. However, many other system elements can be considered transducers, and we’ll consider a few in this lecture.

Each of the two ports has a through- and an across-variable. We use the convention that the power into each port (\(\mathcal{P}_1\) and \(\mathcal{P}_2\)) is positive, which has implications for the signs of the power flow variables \(\mathcal{F}_1\), \(\mathcal{F}_2\), \(\mathcal{V}_1\), and \(\mathcal{V}_2\). For an two-port element to transfer power, we have \[\begin{aligned} \mathcal{P}_1 + \mathcal{P}_2 &= 0 \\ \mathcal{F}_1 \mathcal{V}_1 &= -\mathcal{F}_2 \mathcal{V}_2 \Rightarrow \\ \frac{\mathcal{V}_1}{\mathcal{V}_2} = -\frac{\mathcal{F}_2}{\mathcal{F}_1} \quad &\text{and} \quad \frac{\mathcal{V}_1}{\mathcal{F}_2} = -\frac{\mathcal{V}_2}{\mathcal{F}_1}.\end{aligned}\] We define the transformer ratio \(TF\) to be \[\begin{aligned} TF \equiv \frac{\mathcal{V}_1}{\mathcal{V}_2} = -\frac{\mathcal{F}_2}{\mathcal{F}_1}. \end{aligned}\] Furthermore, we define the gyrator modulus \(GY\) to be \[\begin{aligned} GY \equiv \frac{\mathcal{V}_1}{\mathcal{F}_2} = -\frac{\mathcal{V}_2}{\mathcal{F}_1}. \end{aligned}\]

For an ideal transducer—one that is linear, time-invariant, and without power loss—we have only two nontrivial solutions:¹

\[\begin{aligned} \mathcal{V}_2 &= \mathcal{V}_1/TF \\ \mathcal{F}_2 &= -TF\, \mathcal{F}_1 \end{aligned}\]

or

\[\begin{aligned} \mathcal{V}_2 &= -GY\, \mathcal{F}_1 \\ \mathcal{F}_2 &= \mathcal{V}_1/GY. \end{aligned}\]

For a given element, if the solution with \(TF\) is a good model, we call that element a transformer. If the \(GY\) solution is a good model, we call it a gyrator.

Example 4.1

Consider a DC motor with rotor radius r, number of coil turns N, background field B, and rotor length ℓ. The torque T of a DC motor is related to its coil current i by the relation $$\begin{aligned} T = -2 r N B \ell i. \end{aligned}$$

1. Determine if DC motors are transformers or gyrators.

2. Find TF or GY.

3. Derive the relation between the voltage v and the angular velocity Ω across the motor using the assumption that it is an ideal transducer.

Example 4.2

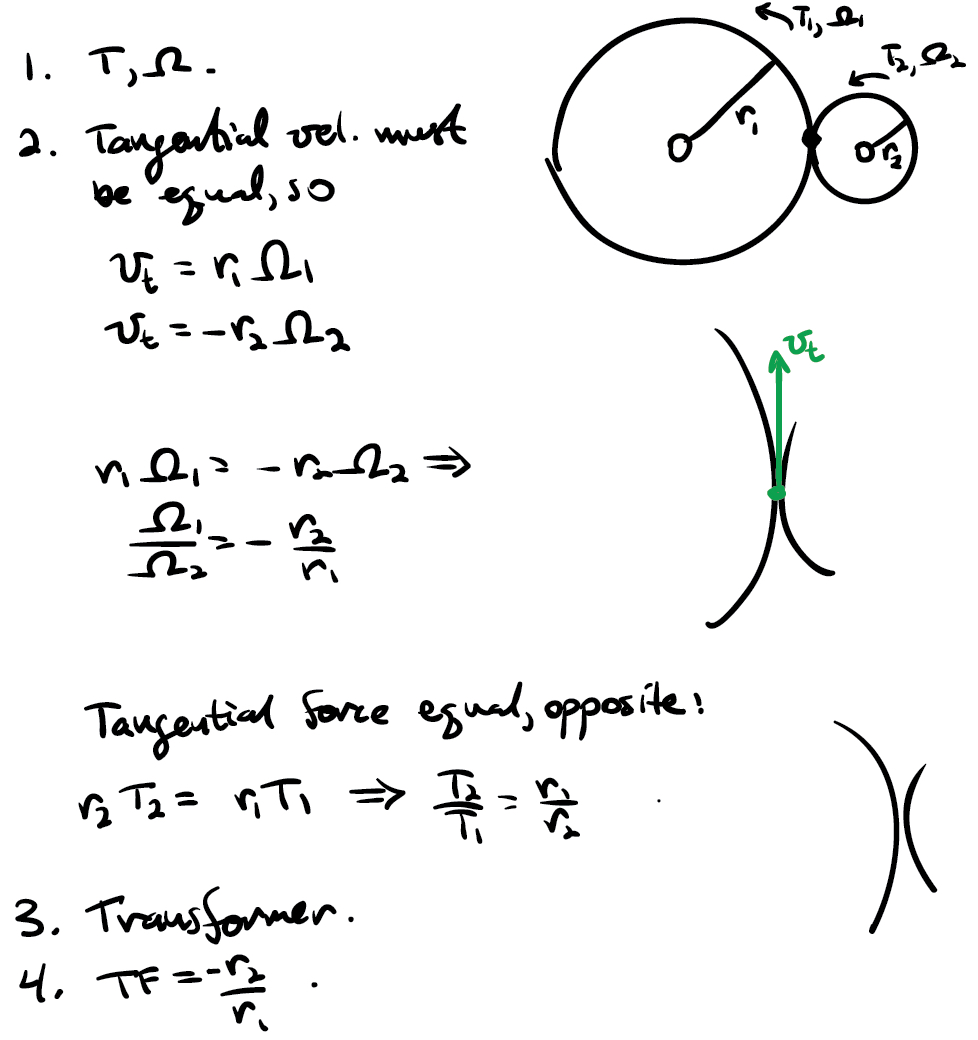
Consider two gears with radii r₁ and r₂ and number of teeth n₁ and n₂.

1. Determine the power flow variables for gears.

2. Write two independent equations relating the power flow variables.

3. Determine if gears are transformers or gyrators.

4. Find TF or GY.

for velocity, tangential velocity must be equal

for torque, tangential force must be equal

the number of teeth ratio is equal because that’s how we make gears ... the radius ratio is equal to the teeth ratio (has to be because the gears need to mesh)